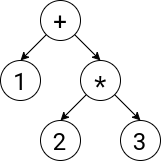
Parsing an expression like 1+2*3 requires a complex representation on memory. Just looking at it we think that it's pretty simple, but there is some hidden hierarchy that we have to pay attention to, like the fact that first we have to compute 2*3 and then add 1 to it. To represent that in a data structure the best thing we can come up to is a tree, as seen in the next figure:  As you can see the leaves of the tree are literals and the root and intermediate nodes are operations that have to be applied from the bottom up. That means that we traverse the tree until we reach the bottom and start computing the results by going up.

> Not all operations are created equal. We have to define how each node fits into the tree. I'll use the following syntax: Binary -> left expr, operator token, right expr. Which means that a binary operation (as we have seen in the image before) links to 2 expressions (left and right) and stores 1 value (operator).

Literal -> value object
# 1, "asd", 5.2, true, false

Binary -> left expr, operator token, right expr
# 1+2, 3*3, 4^2+1

Grouping -> expression expr
# (1+2)

Logical -> left expr, operator token, right expr
# true or false, false and true

Unary: operator token, right expr
# not true, -5

List -> elements []expr
# [1, 2, 3, [4], "asd"]

Dictionary -> elements []expr
# {"a": 1, "b": 2, 3: 4}

Access -> object expr, slice expr
# [1, 2, 3][0], {"a":1}["a"]

Slice -> first expr, second expr, third expr
# [1, 2, 3, 4, 5, 6][1:4:2]

To traverse the syntax tree we need a pattern that's uniform and easily scalable when we have to add other types of expressions and statements. For that we'll use the Visitor Pattern.

First we need an interface for the expression that allows a visitor to visit it.

type expr interface {
    accept(exprVisitor) interface{}
}

An expression visitor should have a method for each kind of expression it has to visit.

type exprVisitor interface {
    visitLiteralExpr(expr expr) interface{}
    visitBinaryExpr(expr expr) interface{}
    visitGroupingExpr(expr expr) interface{}
    visitLogicalExpr(expr expr) interface{}
    visitUnaryExpr(expr expr) interface{}
    visitListExpr(expr expr) interface{}
    visitDictionaryExpr(expr expr) interface{}
    visitAccessExpr(expr expr) interface{}
    visitSliceExpr(expr expr) interface{}
}

Then we have to define a type for each kind of expression that implements expr interface. For example, this is the implementation for a binary expression:

type binaryExpr struct {
    left expr
    operator *token
    right expr
}

func (s *binaryExpr) accept(visitor exprVisitor) R {
    return visitor.visitBinaryExpr(s)
}

For all other expressions the definition is practically the same.

To finish this chapter, let's define a visitor that allows you to print the syntax tree in a lisp-like syntax, ex: (+ 1 2). Here is the implementation of the string visitor for a binary expression:

type stringVisitor struct{}

func (v stringVisitor) visitBinaryExpr(expr expr) R {
    binary := expr.(*binaryExpr)
    return fmt.Sprintf("(%s %v %v)", binary.operator.lexeme, binary.left.accept(v), binary.right.accept(v))
}

You can check out the state of the Grotsky project right here: https://github.com/mliezun/grotsky. Grotsky it's able to parse and print all types of expressions defined in this article right now.

Examples of operations supported:

# Math operations
1+2*3^2-(4+123)/2.6
=> (- (+ 1 (* 2 (^ 3 2))) (/ (+ 4 123) 2.6))

# Logical operations
true or false
=> (or true false)

# Comparisons
1 == 1 and (1 > 3 or 11/5.5 <= 3+2^2 and 1 != 2)
=> (and (== 1 1) (or (> 1 3) (and (<= (/ 11 5.5) (+ 3 (^ 2 2))) (!= 1 2))))

# Lists
[1, 2, [3], "asd"]
=> (list 1 2 (list 3) "asd")

# List slicing
[1,2,3,4][1:3][::2][0]
=> (#0 (#::2 (#1:3 (list 1 2 3 4))))

# Dictionary
{
    1: 2,
    3: 4,
    "asd": 3.14
}
=> (dict 1=>2 3=>4 "asd"=>3.14)

# Dictionary key lookup
{"key":0.6}["key"]
=> (#"key" (dict "key"=>0.6))

That's it for now. In the next chapter we'll traverse the tree but instead of printing we'll execute the operations listed before. If you have questions or suggestions please get in touch.